https://www.acmicpc.net/problem/1920
1920번: 수 찾기
첫째 줄에 자연수 N(1 ≤ N ≤ 100,000)이 주어진다. 다음 줄에는 N개의 정수 A[1], A[2], …, A[N]이 주어진다. 다음 줄에는 M(1 ≤ M ≤ 100,000)이 주어진다. 다음 줄에는 M개의 수들이 주어지는데, 이 수들
www.acmicpc.net
코드
import sys
N = int(sys.stdin.readline().rstrip())
n_list = list(map(int, sys.stdin.readline().rstrip().split()))
M = int(sys.stdin.readline().rstrip())
m_list = list(map(int, sys.stdin.readline().rstrip().split()))
result = []
for i in range(M):
if m_list[i] in n_list:
result.append(1)
else:
result.append(0)
for _ in range(len(result)):
print(result[_])처음에 쓴 틀린 코드입니다. 파이썬의 in을 사용하여 간단하게 푸려고 했지만 괜히 실버4가 아니더군요. 시간초과로 인해 다른 풀이를 생각해봐야 했습니다.
그래서 찾은 방법은 이진탐색(이분탐색)입니다.
이진 탐색이란 오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는알고리즘 입니다. 처음 중간의 값을 임의의 값으로 선택하여, 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 채택합니다. (출처 : 위키백과)
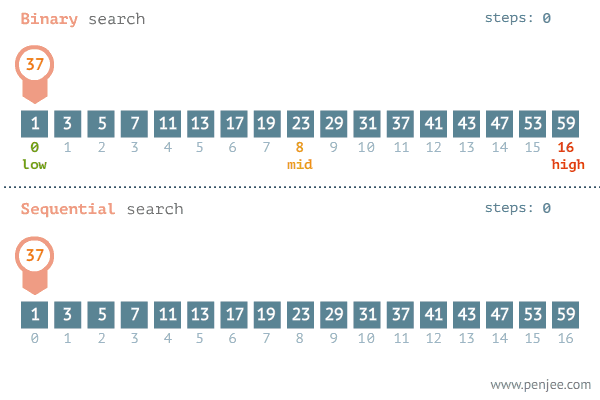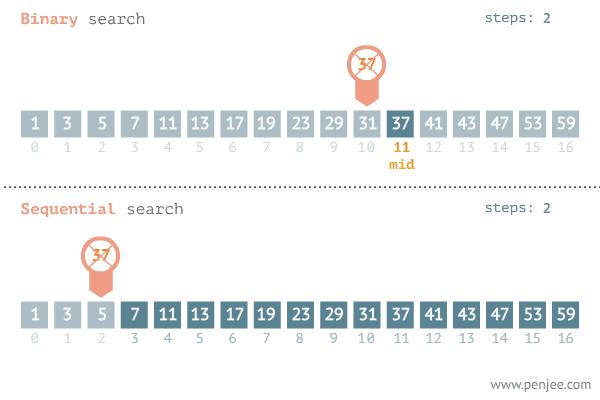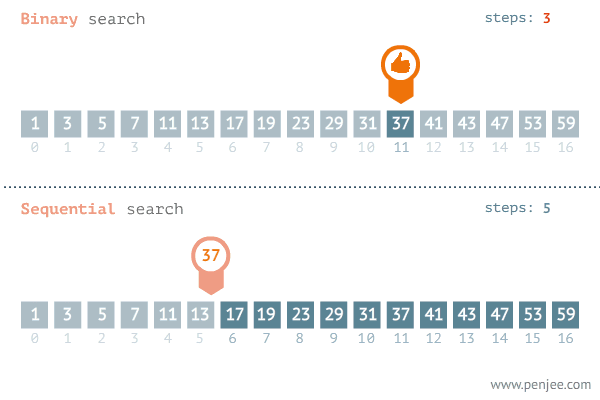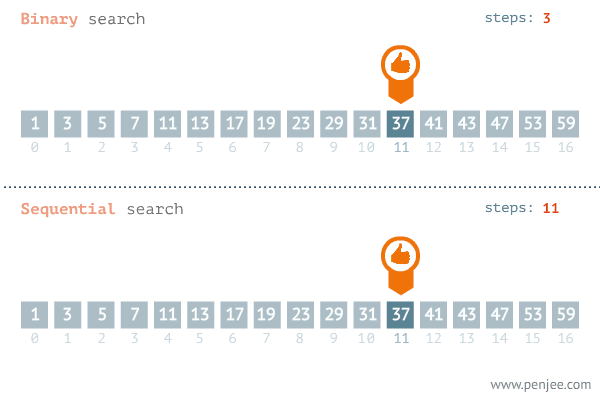
이 이미지를 통해 이진 탐색에 대해 더 쉽게 이해하실 것이라고 생각합니다.
순차 탐색 O(n)에 비해서 이진 탐색은 O(log2n) 이므로 빠르고 효율적입니다.
아래는 이진 탐색을 이용한 코드입니다.
import sys
def binary_search(list, target, start, end):
while start <= end:
mid = (start + end) // 2
if target == list[mid]:
return 1
elif target > list[mid]:
start = mid + 1
else:
end = mid - 1
return 0
N = int(sys.stdin.readline().rstrip())
n_list = list(map(int, sys.stdin.readline().rstrip().split()))
M = int(sys.stdin.readline().rstrip())
m_list = list(map(int, sys.stdin.readline().rstrip().split()))
n_list.sort()
for i in range(M):
print(binary_search(n_list, m_list[i], 0, N-1))이진 탐색을 하기 위해서는 오름차순으로 정렬이 되어있는 리스트가 있어야 하기에 메인 코드에 보시면 처음 입력한 리스트를 sort로 정렬한 것을 보실 수 있습니다.
후에 binary_search라는 이진탐색 함수로 이동하게 됩니다.
이진 탐색 함수는 탐색할 배열, 타겟, 시작점과 끝점을 파라미터로 받습니다.
탐색할 배열에서 타겟을 찾기 위해서는 시작점과 끝점의 중간점이 필요하기 때문입니다.
만약 타겟이 중간점보다 클 시에는 시작점을 중간점+1 한 곳으로 옮기고, 타겟이 중간점보다 작을 시에는 끝점을 중간점-1한 곳으로 옮깁니다. 만약 타겟과 중간점이 같다면 1을 리턴하고, 끝까지 같은 숫자가 없다면 리스트에 해당 숫자가 없다는 의미이므로 반복문을 나갈 때 0을 리턴합니다.
후기
학기중에 이진탐색이라는 용어를 스터디시간에 듣긴 했는데 지금와서 깨달은 것을 보면 그 때 이해를 하지 못했었나 봅니다. 이해하고 보니 새삼스럽게 재미있네요.
'코딩테스트' 카테고리의 다른 글
| [C] 백준 1459번 - '걷기' 풀이 (0) | 2023.01.13 |
|---|---|
| [Python] 백준 1940번 - '주몽' 풀이 (0) | 2023.01.13 |
| [Python] 백준 2839번 - '설탕 배달' 풀이 (0) | 2023.01.11 |
| [Python] 백준 1316번 - '그룹 단어 체커' 풀이 (0) | 2023.01.10 |
| [Python] 백준 4378번 - '트ㅏㅊ;' 풀이 (1) | 2023.01.10 |