베이즈 분류(Bayes Classification)
- Bayes Classifier (베이즈 분류기)
- 가장 단순한 지도 학습(supervised learing) 중 하나
- 분류 문제를 해결하기 위한 확률적 프레임워크(probabilistic framework)
- 베이즈 정리에 기반한 방법으로, 사후확률 계산 시 조건부 독립을 가정하여 계산을 단순화한 방법
- 조건부 독립의 가정이 비현실적임 → hard assumption
- 조건부 확률(Conditional probability)

P(C ❘ A): A이벤트가 일어난다는 가정하에 C라는 이벤트가 일어날 확률 - 베이즈 정리(Bayes theorem)

- 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리
- 베이즈 확률론 해석에 따르면 베이즈 정리는 사전확률로부터 사후확률을 구할 수 있음
- 베이지안 분류기 (Bayesian Classifiers)
- 각 속성과 클래스 레이블을 임의의 변수(random variable)로 간주
- 속성이 있는 레코드 (A1, A2, ..., An)에서
- 클래스 레이블 C를 예측하는 것이 목표
- 즉, P(C|A1, A2, ... , An)을 최대화하는 C의 값을 찾는 것
→ 데이터에서 P(C| A1, A2, ...,An)을 직접으로 추정할 수 있나?
- 접근법
- 베이즈 이론을 사용하여 C의 모든 값에 대한 사후 확률 P(C | A1, A2, ..., An)를 계산

- P(C | A1, A2, ..., An)를 최대화 하는 C의 값을 선택
- P(A1, A2, ..., An)가 모든 클래스에 대해 상수이기 때문에 P(A1, A2, ...,An|C), P(C)를 최대화 하는 C값을 선택하는 것과 동일함
→ P(A1, A2, ...,An| C)을 어떻게 추정할 것인가?
- 베이즈 이론을 사용하여 C의 모든 값에 대한 사후 확률 P(C | A1, A2, ..., An)를 계산
- 나이브 베이즈 분류 (Naive Bayes Classifier)
- 속성들은 conditionally independent
- 즉, 속성 간에 종속성이 없음
- P(A1, A2, ...,An| Cj) = P(A1|Cj) P(A2|Cj) ... P(An|Cj)
- 모든 Ai와 Cj에 대해 P(Ai| Cj)를 추정하는 것이 가능함
- 만약 P(Cj)∏P(Ai| Cj)이 최대이면 새로운 포인트는 Cj로 추정됨
- 데이터에서 확률을 추정하는 방법

- Class:
P(C) = Nc/N- e.g., P(No) = 7/10, P(Yes) = 3/10
- For discrete(이산형) attributes:
P(Ai | Ck) = |Aik|/Nc- where |Aik| is number of instances that has the attribute Ai and belongs to the class Ck
- e.g., P(Status = Married | No) = 4/7
- For continuous(연속형) attributes:
- Discrete attribute로 변환 (e.g., discretization, two-way split)
- 확률 밀도 추정
- 속성이 정규 분포를 따른다고 가정
- 분포(예, 평균, 표준편차)를 추정하기 위해 데이터를 추정함
- 확률 분포를 알게 되면 이를 이용하여 조건부 확률 P(Ai | C)를 추정하는 것이 가능함
- Normal distribution:

- One for each(Ai, Cj) pair
- e.g., (Income, Class=No)
- If Class = No
- sample mean= 110
- sample variance= 2975

- If Class = No
- 나이브 베이즈 분류 예제

조건부 독립이기에 P(X❘Class=No)를 나누어 쓸 수 있음
- Class:
- 나이브 베이즈
- 단순하고 속도가 빠르며 성능이 우수함
- Isolated noise point에 견고함
- 확률 추정 계산에서 인스턴스를 제외하는 방식으로 누락값(missing value)을 처리하는 것이 가능함
- Irrelevant attribute에 견고함
- 독립 가정이 특정 속성들에 대해서는 성립하지 않을 수 있음 → 한계
K-최근접 이웃 분류 (k-Nearest Neighbor Classification)
- k-최근접 이웃 분류
- 입력
- A set of stored data
- A distance metric to compute the distance between records
어떤 기준으로? → distance metric 유사도를 가진 matrix - The number k of nearest neighbors to retrieve
- 예측
- Compute the distance to other training records

- Compute the distance to other training records
- k-Nearest Neighbors
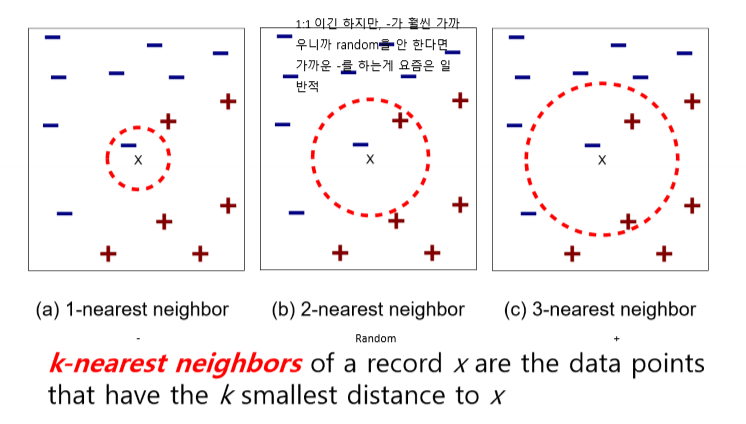
- k-NN Classification
- Compute the distance between two points (e.g., Euclidean distance)

- Determine the class from the nearst neighbor list
- Take the majority vote of class labels among the k-nearest neighbors
→ 더 많은 클래스 선택 - Weight the vote according to distance: weight factor w = 1/d^2
→ 더 가까운 이웃일 수록 d가 이웃까지의 거리일 때, 가중치 1/d^2를 줌
- Take the majority vote of class labels among the k-nearest neighbors
- Compute the distance between two points (e.g., Euclidean distance)
- k-NN 주요 이슈
- The value of k
- If k is too small, classfication is sensitive to noise points
- If k is too large, a neighborhood may include points from other classes

resolution(밀도)에 의해 범위에 따라 달라짐. 가장 좋은 방법은 데이터에 대한 insight가 있는 사람이 결정하는 게 좋음
- Scaling
- Attributes may have to be scaled to prevent distance measures from being dominated by one of the attributes
→ scaling 대신 nomalization(정규화)를 하여 모든 attribute의 영향력을 동일하게 함
- Attributes may have to be scaled to prevent distance measures from being dominated by one of the attributes
- High-dimensional data
- Curse of dimensionality
→ dimensionality reduction으로 해결
- Curse of dimensionality
- The value of k
- 입력
서포트 벡터 머신 (Support Vector Machines)
- 선형으로 분리가 가능한 경우

- Find the hyperplane(decision boundary) that maximizes the margin → B1 is better than B2
- SVM searches for the hyperplane with the largest margin, i.e., maximum marginal hyperplane(MMH)
→ margin이 제일 큰 hyperplane 선택
- Soft Margin
- If there exists no hyperplane that can split the "yes" and "no" examples, the soft margin method will choose a hyperplane that splits the examples as cleanly as possible, while still maximizing the distance to the nearst cleanly split examples → Allow mislabeled examples
(깨끗하게 분리하게 위해 어느정도의 손실을 냄)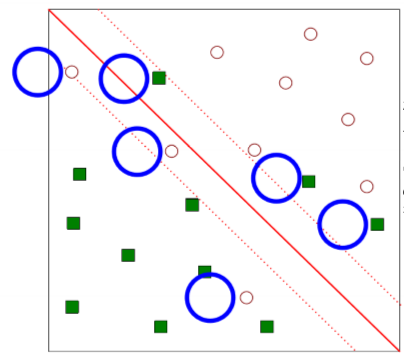
- If there exists no hyperplane that can split the "yes" and "no" examples, the soft margin method will choose a hyperplane that splits the examples as cleanly as possible, while still maximizing the distance to the nearst cleanly split examples → Allow mislabeled examples
- 선형으로 분리가 안 되는 경우
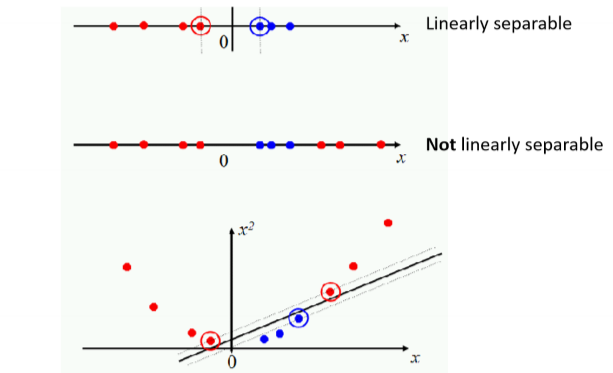
- Projecting data that is not linearly separable into a higher dimensional space can make it linearly separable
→ 차원이 올라갈수록 단점이 많아진다
- Projecting data that is not linearly separable into a higher dimensional space can make it linearly separable
- LIBSVM
- A library for Support Vector Machines
앙상블 방법 (Ensemble Methods)
- 앙상블 방법
- training data로부터 분류기의 set을 구성
- 여러 개의 모델을 조화롭게 학습시켜 그 모델들의 예측 결과들을 이용하는 형태

- 의미가 있는 이유
- 25개의 분류기가 있다고 가정
- 각 분류기의 오류율, ε = 0.35
- 분류기의 오류가 서로 관련이 없다고 가정
- 앙상블 분류기가 잘못된 예측을 할 가능성:


앙상블은 powerful함. 약한 분류기를 많이 써서 error율을 줄일 수 있음
- 25개의 분류기가 있다고 가정
- 배깅 (Bagging)
- 앙상블 투표에서 각 모델을 동일한 가중치로 사용
- training data set을 random하게 구성한 부분 집합을 사용하여 앙상블 각 모델을 훈련시킴
- 예, Random Forests
- 무작위 결정 트리를 배깅과 결합하여 분류 정확도를 매우 높이는 형태
- 부스팅 (Boosting)
- 이전 모델이 잘못 분류한 training data set의 인스턴스를 강조하기 위해 각각의 새 모델 인스턴스를 훈련해서 앙상블을 점진적으로 구축
- 경우에 따라 Bagging 보다 더 나은 정확성을 보여주기도 하지만 일반적으로는 Overfitting을 유발할 가능성이 높음
- 예, AdaBoost
- Bagging vs Boosting

Bagging: parallel / Boosting: sequential - Bagging
- 개별 training data set와 분류기는 독립적
→ 분류기를 나누고 paraller 해서 각각
- 개별 training data set와 분류기는 독립적
- Boosting
- 부스팅에서는 모든 training data 예제가 각 반복에서 사용됨
- 연속적인 분류기는 이전의 분류기에 의존적
- 즉, 다음 분류에 집중할 항목을 결정하기 위해 이전 분류 결과의 오류를 확인
- 다만, 판별이 어려운 예제에 대해 더 많은 가중치를 부여함
- Bagging
- Random Forests
- 훈련을 통해 구성해놓은 다수의 나무들로부터 분류 결과를 취합해서 결론을 얻는 방법

- 훈련을 통해 구성해놓은 다수의 나무들로부터 분류 결과를 취합해서 결론을 얻는 방법
- Random Forests에서 Training
- 각 트리의 생성
- 훈련 데이터 셋의 수가 N인 경우 원래 데이터에서 교체하여 무작위로 N 사례를 샘플링하며 이것이 트리를 구성하기 위한 training data set이 됨
- N이 증가함에 따라 1-e^(-1)≒63.212% 이기 때문에 훈련 인스턴스의 약 63%만이 평균적으로 샘플링 됨
(자동적으로 나머지는 test data가 됨)
- N이 증가함에 따라 1-e^(-1)≒63.212% 이기 때문에 훈련 인스턴스의 약 63%만이 평균적으로 샘플링 됨
- M개의 입력 변수가 있는 경우, m(≪M) 변수들이 M변수들 중에 임의로 선택되고 이 m변수에서 가장 잘 나누어지는 분할 방법이 사용됨
- m의 값은 forest가 생성되는 동안 일정하게 유지됨
- 각 트리는 가능한 최대 레벨로 생성됨
- 훈련 데이터 셋의 수가 N인 경우 원래 데이터에서 교체하여 무작위로 N 사례를 샘플링하며 이것이 트리를 구성하기 위한 training data set이 됨
- Forest의 오류율(error rate)은 다음 두 가지에 따라 다름
- Forest에서 두 트리 간 상관 관계 → 상관 관계를 높이면 forest의 오류율 증가
- Forest에서 개별 트리의 강도 → 개별 트리의 강도를 높이면 forest의 오류율 감소
- m을 줄이면 상관관계와 강도가 모두 줄어들고 m을 증가시키면 상관관계와 강도가 모두 증가
→ OOB 오류율을 사용하면 범위 내 m 값을 빠르게 찾을 수 있음
- 각 트리의 생성
- Out-of-Bag (OOB) 에러 추정
- 교차 검증 또는 별도의 test data set이 불필요한 특징을 지미
- 각 트리는 원래 데이터와 다른 bootstrap 샘플을 사용하여 구성도미
- Bootstrap 샘플에서 약 1/3 (또는 37%) 정도의 케이스들이 남겨짐
→ OOB 인스턴스들 → test data set - 각 실행마다, 가장 많은 투표를 받은 클래스를 선택하고 실행 횟수에 비례해서 선택한 클래스와 실제 클래스와 같지 않은 비율을 전체 케이스들에 대해 계산한 것이 OOB error estimate가 됨
- decision tree(CART)와 Random Forest 비교

- Decision boundaries of CART and random forest
→ tree가 많아서 세밀한 boundary 형성이 가능
- Decision boundaries of CART and random forest
- AdaBoost

- AdaBoost 예제

- Original training set: equal weights to all training samples
- Round 1
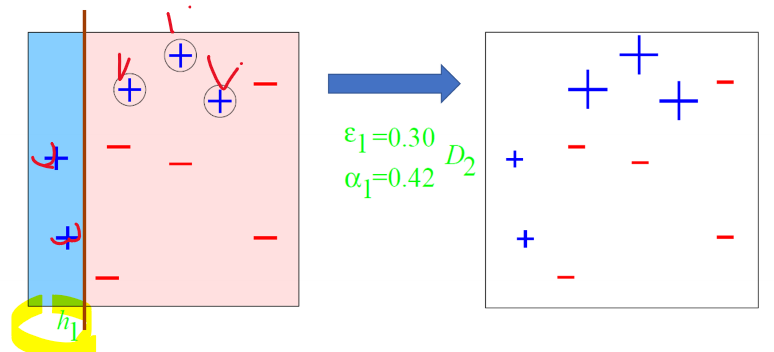
- Round 2

- Round 3

- Final Hypothesis

- AdaBoost 예제
'빅데이터' 카테고리의 다른 글
| [빅데이터분석] 7장. 클러스터링 (0) | 2024.06.09 |
|---|---|
| [빅데이터분석] 5장. 분류(1) (0) | 2024.06.08 |
| [빅데이터분석, R] 연관 분석 (0) | 2024.04.21 |
| [빅데이터분석, Python] 연관 분석 (Assocination Analysis) (0) | 2024.04.21 |
| [빅데이터분석, Python] 전처리(Data-Preprocessing) (0) | 2024.04.21 |



