클러스터링
- 클러스터 분석(Cluster Analaysis)
- 클러스터: a collection of data objects
- 서로 유사한 데이터 객체들은 같은 그룹(클러스터)에 속함
- 서로 유사하지 않는 객체들은 서로 다른 그룹(클러스터)에 속함
- 클러스터 분석
- 데이터 간 유사도(distance)를 측정하여 유사한 데이터 객체들을 같은 클러스터에 할당하는 작업
- 사전 정의된 클래스가 없는 대표적인 비지도 학습 기법 중 하나
- 클러스터: a collection of data objects
- 전처리 목적의 클러스터링
- 요약(Summarization): Preprocessing for regression, PCA, classification, and associate analysis
- 이상치 발견(Outlier detection): Outliers are often viewed as those "far away" from any cluster
- 이상적인 클러스터링
- 이상적인 클러스터링은 정답이 없기 때문에 주관적이며 정의하는 것이 어려움

- 일반적으로 말하는 이상적인 클러스터링

- Intra-cluster distances: 같은 cluster에 있는 object 사이의 distances
- Inter-cluster distances: 서로 다른 cluster 사이의 distances
- 이상적인 클러스터링은 정답이 없기 때문에 주관적이며 정의하는 것이 어려움
- 클러스터 분석의 고려 사항
- 분할 기준 (Partitioning criteria)
- Single level vs. Hierarchical partitioning
- 클러스터의 분리 (Speration of clusters)
- Exclusive vs. Non-exclusive (non-exclusive는 overlapping이 가능)
- 유사도 측정 (Similarity measure)
- Distance-based vs. Connectivity-based (밀도)
- 클러스터링 공간 (Clustering space)
- Full space (모든 object가 하나의 cluster에 들어감) vs. Subspaces (모든 object가 cluster에 들어가지 않아도 됨)
- 분할 기준 (Partitioning criteria)
- 주요 클러스터링 방법
- 분할 기반 (Partitioning-based)
- Construct various partitions and then evaluate them by some criterion, e.g., minizing the sum of square errors
- 계층적 (Hierarchical)
- Create a hierarchical decomposition of the set of data (or objects) using some criterion
- 밀도 기반 (Density-based)
- Based on connectivity and density functions
- 그리드 기반 (Grid-based)
- 모델 기반 (Model-based)
- 빈발 패턴 기반 (Frequent pattern-based)
- 사용자 가이드 또는 제약 기반 (User-guided or constraint-based)
- 링크 기반 (Link-based clustering)
- 분할 기반 (Partitioning-based)
파티션 방법 (Partitioning Methods)
- 개념
- n개의 객체를 대상으로 k개의 파티션(즉, 클러스터)을 구성
- Each group must contain at least one object
- Each object must belong to exactly one group (can be relaxed in some fuzzy techinques)
→ exclusive 함 (non-exclusive로도 변환 가능하나, 기본적으로는 exclusive)
- 초기 파티션을 만든 다음 반복적인 재배치를 통해 파티션을 개선
- n개의 객체를 대상으로 k개의 파티션(즉, 클러스터)을 구성
- 방법
- k-means
- k-medoids or PAM
- k-Means 클러스터링
- step1) 전체 data set에서 k개의 object를 초기 cluster 중심점으로 선택(random 선택)
- step2) 각 object를 가장 가까운 cluster에 할당 (또는 재할당)
- step3) cluster의 mean(각 cluster에 속하는 object들의 mean 값)을 업데이트
- step4) 수렴 조건을 만족할 때 까지 2~3을 반복
- 평가 기준 (Evaluation Criterion)
- 알고리즘은 제곱 오차의 합을 최소화하는 k개의 clusterf를 결정하는 형태

- p: a point(object) in a cluster Ci
- mi: the mean of a cluster Ci
- k개의 클러스터를 가능한 Compact하고 멀리 떨어지게(separate)함
- 알고리즘은 제곱 오차의 합을 최소화하는 k개의 clusterf를 결정하는 형태
- k-Means 클러스터링의 예

k = 3으로 지정 
- 초기 중심점 선택의 영향

initial point를 적절하게 설정하는 것이 중요하다 - 특징
- 효율성(efficient)
- O(tkn), where n is # of objects, k is # of clusters, and t is # of iterations; usually, k, t ≪ n
→ O(n)의 시간 복잡도. n: 데이터의 객체 수, k: 전체 클러스터의 수, t: iteration 반복 수행 횟수)
- O(tkn), where n is # of objects, k is # of clusters, and t is # of iterations; usually, k, t ≪ n
- 종종 local optimal에 빠짐 → initial point가 중요
- 효율성(efficient)
- 한계점
- 연속적인 공간에 있는 객체들에 대해서만 적용이 가능함
- k를 미리 지정해주어야 함
- 볼록하지 않은 (non-convex)모양, 크기나 밀도가 다른 클러스터를 발견하기에 적합하지 않음
- 노이즈(noise)나 이상치(outlier)에 민감함
- k-Means의 한계점: Different Sizes

- k-Means의 한계점: Different Density
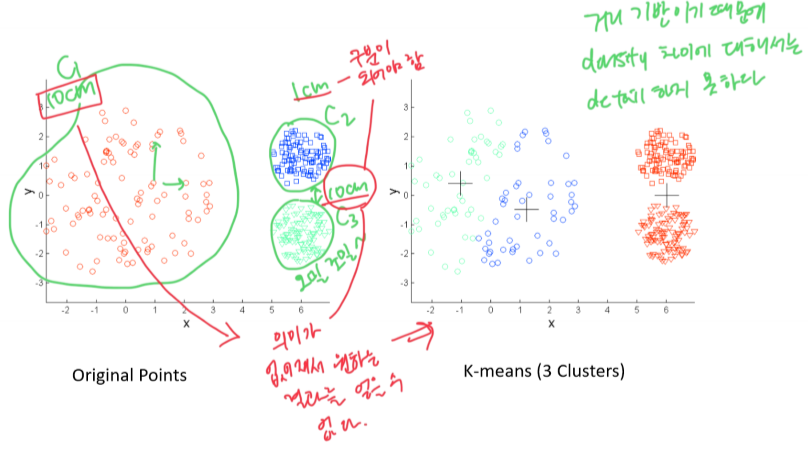
- k-Means의 한계점: Non-Convex Shapes

- k-Means 방법의 문제점
- 이상치(outlier)에 민감함
- Since an object with an extremely large may substantially distort the distribution of the data
→ 해결책: k-Medoids - Instead of taking the mean value of the objects in a cluster as a reference point, medoids can be used
- medoid: the most centrally loacated object in a cluster
→ 평균이 아닌 클러스터 가운데 위치하는 object를 이용
- medoid: the most centrally loacated object in a cluster
- Since an object with an extremely large may substantially distort the distribution of the data
- 이상치(outlier)에 민감함
- PAM: 대표적인 k-Medoids 알고리즘
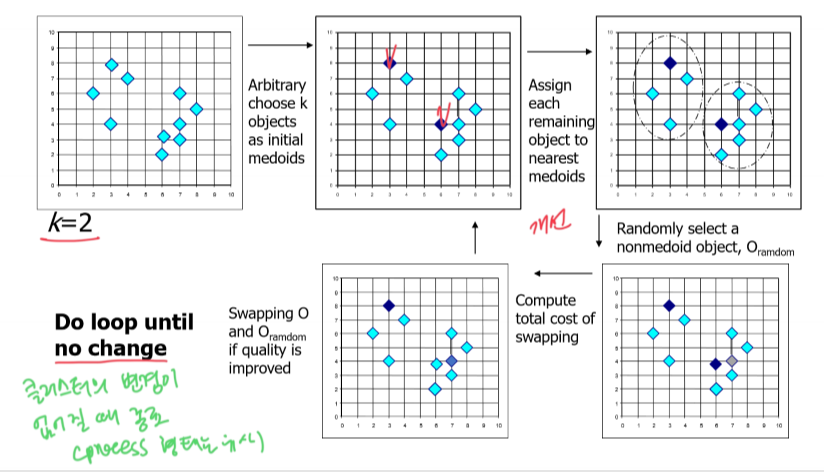
- k-Medoids 클러스터링
- k-Medoids 클러스터링: 클러스터에서 대표 객체(medoids)를 찾음
- PAM(Partitioning Around Medoids, Kaufmann & Rousseeuw 1987): 초기 medoids에서 시작해서 특정 조건을 수렴할 때까지 반복적으로 결과 클러스터의 전체 거리를 개선하는 경우에 대해 medoids를 변경
- PAM은 소규모 data set에서는 잘 동작하지만 대규모 data set에 대해서는 계산 복잡도로 인해 잘 동작하지 않는 경향이 있음
- PAM의 효율성(efficiency)를 향상시킨 알고리즘
- CLARA
- CLARANS
- k-Medoids 클러스터링: 클러스터에서 대표 객체(medoids)를 찾음
계층적 방법 (Hierarchical Methods)
- 계층적 클러스터링
- 계층적 트리 또는 중첩 클러스터(nested cluster)를 생성

첫 번째 그림은 dendogram - 일반적으로 distance matrix를 클러스터링의 기준으로 사용함
- 계층적 트리 또는 중첩 클러스터(nested cluster)를 생성
- 계층적 클러스터링의 장점
- 클러스터의 개수를 미리 지정하지 않아도 됨
- Dendogram을 정정 수준으로 cut하면 원하는 수의 클러스터들을 얻는 것이 가능함
- 계층 트리는 의미 있는 분류 체계와 대응되기도 함
- 클러스터의 개수를 미리 지정하지 않아도 됨
- 두 가지 접근 방식
- 병합형 (Agglomerative)
- Start with the points as individual clusters
- At each step, merge the closest pair of clusters until only one cluster (or k clusters) is left
→ k개의 cluster로 시작하여 점점 뭉쳐가는 방식
- 분할형 (Divisive)
- Start with one, all-inclusive cluster
- At each step, split a cluster until each cluster contains a point (or there are k clusters)
→ 하나의 cluster로 시작하여 점점 쪼개가는 방식
- 병합형 (Agglomerative)
- 병합형 클러스터링 (Agglomerative Clustering)
- Agglomerative is more popular than divisive 병합형이 분할형보다 많이 사용됨
- The key operation is the computaion of the similarity of two clusters (유사도 계산)
- Differnet approaches to defining the distance between clusters distinguish the different algorithms
→ 다양한 유사도 계산 기준이 있고, 각 기준에 따라 계산 결과가 달라짐
- Differnet approaches to defining the distance between clusters distinguish the different algorithms
- 시작 상황 (Starting Situation)
- Start with clusters of individual points and a distance matrix
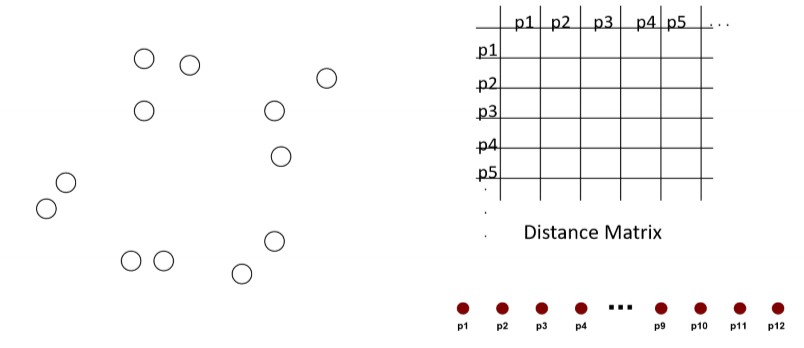
- Start with clusters of individual points and a distance matrix
- 중간 상황 (Intermediate Situation)
- After some merging steps, we have some clusters

- After some merging steps, we have some clusters
- 통합 이후 (After Merging)
- We want to merge the closet two clusters (C2 and C5) and update the distance matrix

- We want to merge the closet two clusters (C2 and C5) and update the distance matrix
- 클러스터 유사도 정의 방법
- Single link (MIN)
- Complete link (MAX)
- Average
- Centroid

- Single link (MIN)

- Complete link (MAX)

- Average

- Centroid

- 계층적 클러스터링의 확장
- 병합형 클러스터링의 주요 단점
- Can never undo what was done previously
→ 한 번 병합하면 쪼갤 수 없음. 병합 이전 결과를 저장하지 않기 때문. complexity가 높아서 저장이 불가능. - Do not scale well: time complexity of at least O(n^2), when n is the number of total objects
→ complexity가 높아서 대규모 dataset에서는 사용이 어려움.
- Can never undo what was done previously
- 계층적 방법과 거리 기반 방법의 통합
- BIRCH
- CHAMELEON
- 병합형 클러스터링의 주요 단점
밀도 기반 방법 (Density-Based Methods)
- 밀도를 기준으로 클러스터를 확장해 나가는 방법
- 특징
- Discover clusters of arbitrary shape
→ cluster의 shape에 상관 없음. 밀도만 잘 되어있으면 됨. - Handle noise
- One Scan
→ k-means: t번 iteration / dbscan은 한 번만 방문. one scan - Need density parameters as termination condition
→ parameters(Eps, MinPts)를 정하는 것이 어려움
- Discover clusters of arbitrary shape
- 관련 연구
- DBSCAN
- OPTICS
- DENCLUE
- CLIQUE
- DBSCAN(Density-Based Spatial Clustering of Applications with Noise)
- 두개의 파라미터:
- Eps: Maximum radius
- MinPts: Minimum number of points in an eps-neighborhood of that point
→ 반경 안에 들어오는 point가 몇 개인가

- Directly density-reachable: A point p is directly density-reachable from a point q w.r.t. Eps, MinPts
→ point p가 point q의 반경에 들어오고, 점 q가 코어점일 때, point p가 point q로부터 directly density-reachable한 관계에 있다고 한다. (반대의 경우는 성립하지 않음)

- Density-Reachable / Density-Connected
- Density-reachable
- A point p is density-reachable from a point q w.r.t. Eps, MinPts if there is a chain of points p1, p2, ..., pn , p1 = q , pn = p such that pi+1 is directly density-reachable from pi
→ point p 와 point q 사이에 p1, p2, ..., pn, p1 = q, pn=p 들이 있고, pi+1이 점 pi로부터 직접적으로 density-reachable하면, 점 p는 점 q로부터 density-reachable한 관계에 있다고 한다.
순서(chain)가 있음
- A point p is density-reachable from a point q w.r.t. Eps, MinPts if there is a chain of points p1, p2, ..., pn , p1 = q , pn = p such that pi+1 is directly density-reachable from pi
- Density-connected
- A point p is density-connected to a point q w.r.t. Eps, MinPts if there is a point o such that both p and q are denstiy-reachable from o w.r.t. Eps and MinPts
→ 만약 두 점 p와 q가 모두 어떤 점 o로부터 반경 내 MinPts 조건 하에 density-reachable하면 점 p는 점 q와 반경 내 MinPts 조건 하에 density-connected 되었다고 한다.
순서 없음. 중간에 매개가 있으면 가능
- A point p is density-connected to a point q w.r.t. Eps, MinPts if there is a point o such that both p and q are denstiy-reachable from o w.r.t. Eps and MinPts
- Density-reachable
- 두개의 파라미터:
- 개념
- 클러스터는 밀도 기반 연결 포인트들의 최대 집합으로 정의됨
- 노이즈가 존재하는 공간 DB에서 임의의 형태 클러스터를 발견하는 것이 목적
- DBSCAN 실행 예시




- 특징
- 복잡도
- O(n^2) or O(nlogn) if an index is used, when dimensionality ≤ 2
- 장점
- Does not require you to know the number of clusters
- Can find arbitrarily shaped clusters
- Has notion of noise
- Mostly insensitive to the ordering of the points in the database
- 단점
- Hard to determine the proper parameter values (Eps, MinPtr)
- Cannot cluster data sets well with large differeces in densities
- 복잡도
- parameter에 대한 민감도

- Eps과 MinPts를 결정하는 방법
- Sorted k-dist graph
클러스터 평가
- 클러스터의 유효성 (Cluster Validity)
- 지도학습 기반의 분류 기법에서는 모델을 평가하는 다양한 척도들이 존재함
→ accuracy, precision, recall - 클러스터 분석에서도 지도학습 기반의 분류와 마찬가지로 결과 클러스터가 얼마나 잘 되었는가에 대한 평가 척도가 필요함
- 지도학습 기반의 분류 기법에서는 모델을 평가하는 다양한 척도들이 존재함
- 클러스터 유효성 평가에 대한 다양한 측면
- Determining the clustering tendency of a set of data, i.e., distinguishing whether non-random structure actually exists in the data
- Determining the correct number of clusters
- Evaluating how well the results of a cluster analysis fit the data without references to external information
- Comparing the results of a cluster analysis to externally known results
- Comparing two sets of clusters to determine which is better
- 클러스터 유효성 평가 기준
- Unsupervised measure, Internal index: Used to measure the goodness of a clustering structure without respect to external information
- Measures of cluster cohesion (compactness, tightness)
- Measures of cluster separation (isolation)
- Supervised measure, External index: Used to measure the extent to which cluster labels match externally supplied class labels
- e.g., Entropy
- Relative measure: Used to compare two different clustering results (i.e., clusters)
- Can be either a unsupervised or supervised measure
- Unsupervised measure, Internal index: Used to measure the goodness of a clustering structure without respect to external information
- Unsupervised Cluster Evaluation: Cohesion and Speration
→ Cohesion: intra-cluster / Seperation: inter-cluster
- Cohesion: SSE

- Seperation: SSB

- Note: Minimizing SSE(cohesion) is equivalent to maximizing SSB(seperation)
- Cohesion: SSE
- Silhouette Coefficient
- The silhouette coefficient combines the ideas of both cohesion and seperation (but for individual points)
- For the i-th object,

- The value of si is between -1 and 1; when it tis closer to 1, the cluster result is better
→ silhouette coefficient가 크면 좋음(너무 큰 건 좋지 않음). Eps, MinPts를 silouette coefficient를 통해 정하게 됨
'빅데이터' 카테고리의 다른 글
| [빅데이터분석] 6장. 분류(2) (0) | 2024.06.08 |
|---|---|
| [빅데이터분석] 5장. 분류(1) (0) | 2024.06.08 |
| [빅데이터분석, R] 연관 분석 (0) | 2024.04.21 |
| [빅데이터분석, Python] 연관 분석 (Assocination Analysis) (0) | 2024.04.21 |
| [빅데이터분석, Python] 전처리(Data-Preprocessing) (0) | 2024.04.21 |



